Home Geometry Which Statement Describes This Pair Of Congruent Triangles

Which Statement Describes This Pair Of Congruent Triangles

May 7, 2024

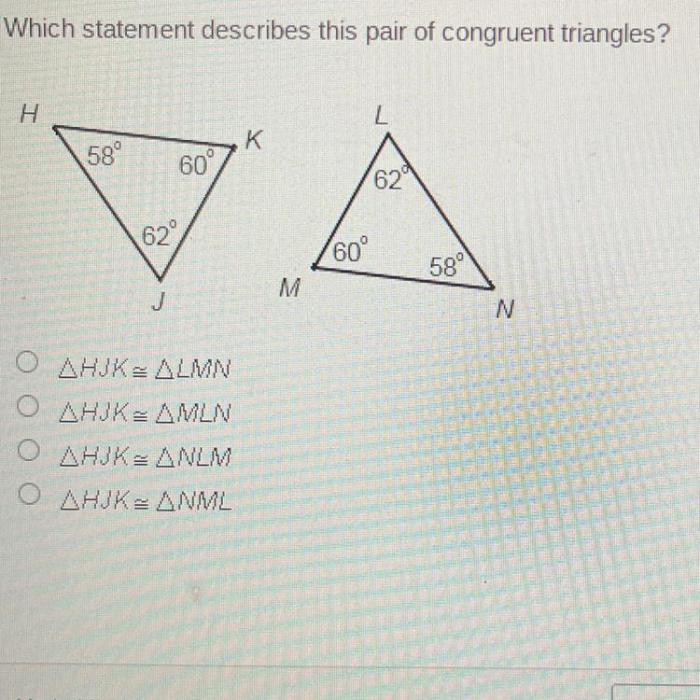
Which statement describes this pair of congruent triangles sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail and brimming with originality from the outset. Embark on an intellectual journey as we delve into the captivating world of congruent triangles, unraveling their properties, exploring methods of identification, and deciphering the enigmatic statements that define their very essence.

Prepare to be captivated as we unveil the secrets that lie within these geometric marvels.

In the realm of geometry, congruent triangles stand as beacons of equality, their corresponding sides and angles mirroring each other with impeccable precision. Understanding the statements that describe these congruent triangles is paramount to unlocking their geometric significance and unraveling the mysteries they hold.

Congruent Triangle Properties

Which statement describes this pair of congruent triangles

Congruent triangles are triangles that have the same shape and size. They have the same corresponding angles and sides. Congruent triangles can be identified using various methods, such as the side-angle-side (SAS) method, the angle-side-angle (ASA) method, and the side-side-side (SSS) method.

Properties of Congruent Triangles, Which statement describes this pair of congruent triangles

Congruent triangles have the following properties:

  • Corresponding angles are congruent.
  • Corresponding sides are congruent.
  • The triangles have the same shape and size.

These properties can be used to determine whether two triangles are congruent. For example, if two triangles have three pairs of congruent corresponding angles, then the triangles are congruent.

Identifying Congruent Triangles

Sas congruence similarity cuemath δabc pq

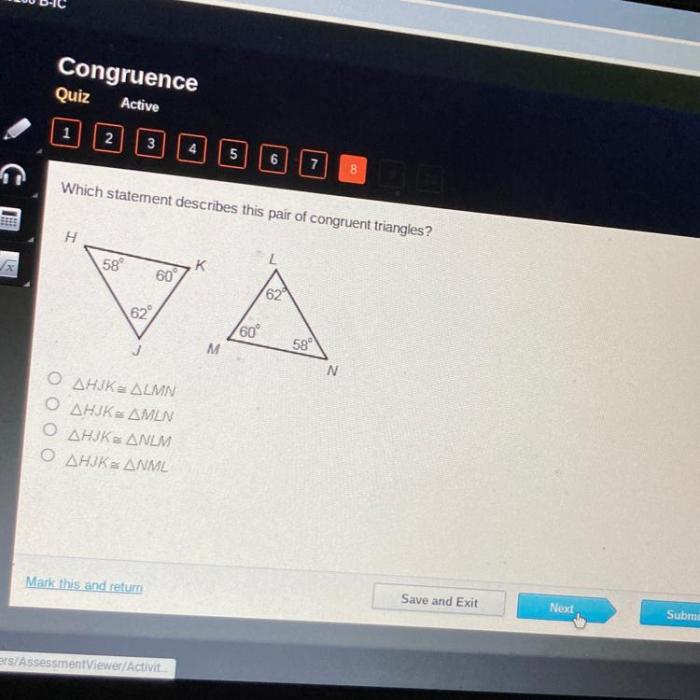
There are several methods that can be used to identify congruent triangles. These methods include:

  • Side-Angle-Side (SAS) Method:If two triangles have two pairs of congruent corresponding sides and a pair of congruent corresponding angles, then the triangles are congruent.
  • Angle-Side-Angle (ASA) Method:If two triangles have two pairs of congruent corresponding angles and a pair of congruent corresponding sides, then the triangles are congruent.
  • Side-Side-Side (SSS) Method:If two triangles have three pairs of congruent corresponding sides, then the triangles are congruent.

The following table compares the different methods used to identify congruent triangles:| Method | Conditions ||—|—|| SAS | Two pairs of congruent corresponding sides and a pair of congruent corresponding angles || ASA | Two pairs of congruent corresponding angles and a pair of congruent corresponding sides || SSS | Three pairs of congruent corresponding sides |

Statements Describing Congruent Triangles: Which Statement Describes This Pair Of Congruent Triangles

Which statement describes this pair of congruent triangles

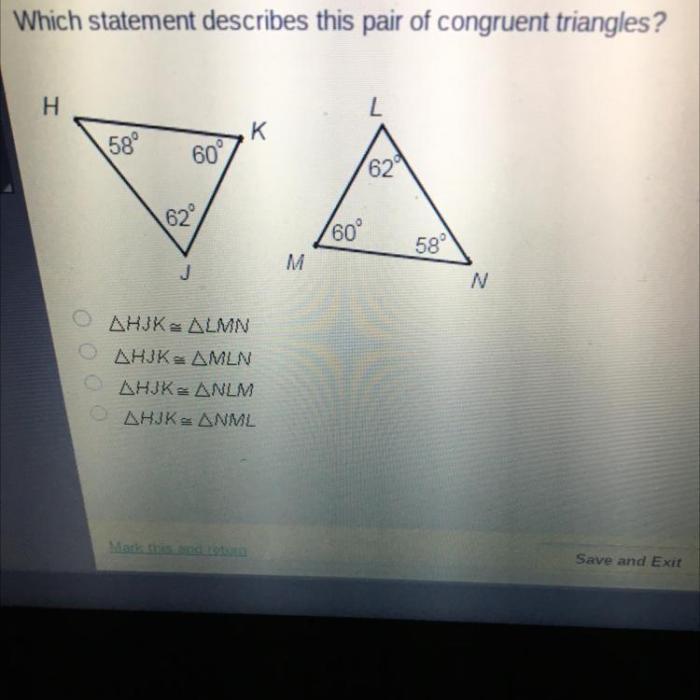
The following statements describe congruent triangles:

  • Triangles that have the same shape and size are congruent.
  • Triangles that have three pairs of congruent corresponding sides are congruent.
  • Triangles that have three pairs of congruent corresponding angles are congruent.
  • Triangles that have two pairs of congruent corresponding sides and a pair of congruent corresponding angles are congruent.
  • Triangles that have two pairs of congruent corresponding angles and a pair of congruent corresponding sides are congruent.

These statements can be used to determine whether two triangles are congruent. For example, if two triangles have the same shape and size, then they are congruent.

Triangle Congruence Theorems

There are several triangle congruence theorems that can be used to determine whether two triangles are congruent. These theorems include:

  • AAS (Angle-Angle-Side) Theorem:If two triangles have two pairs of congruent corresponding angles and a pair of congruent corresponding non-included sides, then the triangles are congruent.
  • HL (Hypotenuse-Leg) Theorem:If two right triangles have congruent hypotenuses and a pair of congruent corresponding legs, then the triangles are congruent.
  • SSS (Side-Side-Side) Theorem:If two triangles have three pairs of congruent corresponding sides, then the triangles are congruent.

The following table summarizes the conditions for each triangle congruence theorem:| Theorem | Conditions ||—|—|| AAS | Two pairs of congruent corresponding angles and a pair of congruent corresponding non-included sides || HL | Congruent hypotenuses and a pair of congruent corresponding legs || SSS | Three pairs of congruent corresponding sides |

Key Questions Answered

What is the significance of congruent triangles?

Congruent triangles play a crucial role in geometry, providing a foundation for understanding geometric relationships and solving complex problems. They are used in various applications, including architecture, engineering, and design.

How can I identify congruent triangles?

There are several methods to identify congruent triangles, including the Side-Side-Side (SSS) Congruence Theorem, the Side-Angle-Side (SAS) Congruence Theorem, and the Angle-Side-Angle (ASA) Congruence Theorem.

What statements describe congruent triangles?

Statements that describe congruent triangles include: “Corresponding sides are equal,” “Corresponding angles are equal,” and “Corresponding parts are equal.”